低調的數學邪惡組織的低調入團測驗解答篇，以下是各題解答。

A1 假面報名者

一共有17280種可能性

詳解：

首先要將每一個區塊做區分，我們先將每一區塊的接觸面的數量寫出來。

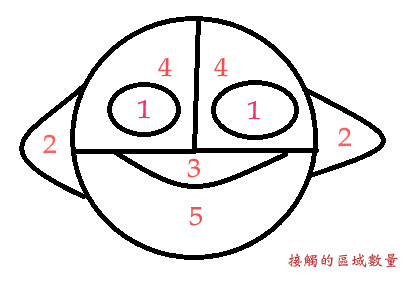
接下來再按照接觸區塊數量由多到少去安排填塞順序，從鄰居最多的開始填色，但是因為眼睛和耳朵的部分比較獨立特殊，所以在填完其他四個區域後再填色。

這邊我們分成A下巴、B左臉、C右臉、D嘴巴、E左眼、F右眼、G左耳、H右耳這幾個部份。

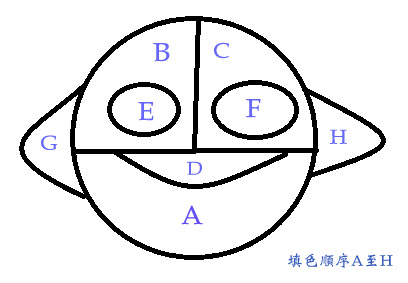
之後再按照A至H的順序去填色，並按照順序去填完這些顏色。

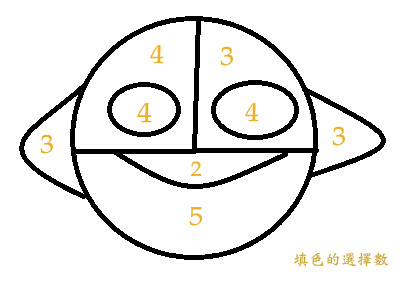
因此全部能填色的總數為5×4×3×2×4×4×3×3＝17280（種）

所以面具有17280種變化的可能性。

A2 走樓梯

能夠上來樓梯到門口的人最多為89人

詳解：

我們可以先簡單的推導一下，若是樓梯只有1階，只會有一種方法， 2階的話，會有1+1、2兩種方法； 3階的話，會有1+1+1、1+2、2+1三種方法； 4階的話，會有1+1+1+1、1+1+2、2+1+1、1+2+1、2+2，五種方法。

根據上述觀察我們發現一件事，1階和2階的方法數合起來會等於3階的方法數，2階和3階的方法數合起來會等於4階的方法數，因此推論5階應該是由3階的數量與4階的數量加起來為8種，6階就會是由5階和4階的方法數加起來，為13種。

以此推論完成了這個表格

1階	2階	3階	4階	5階
1	2	3	5	8
6階	7階	8階	9階	10階
13	21	34	55	89

因此10階的方法數為89。

能夠上來樓梯到門口的人最多為89人。

A3 ０的對應

（D）無意義

詳解：

我們用個簡單的說法來說明次方的意義。

例如當我們用\($3^4$\)去除\($3^4\)時得到的式子是

\(\frac{3^4}{3^4}=3^{4-4}=3^0=1\)

然而0本身是沒辦法去做這件事情，0的任何次方皆無法被當作分母來除，故，零的零次方無意義。

雖然有些數學上會把\(0^0=1 \)來方便於某些計算使用，但是普遍來說（至少以一位國高中來說），零的零次方是毫無意義的。

A4 六弧花

\( 432\sqrt3-144\pi\) 平方公分

詳解：

首先先連接AO、FO，求扇形面積

\(12\times 12\times\frac1 6\times\pi=24\pi\)

再求正三角形AOF的面積

\( \frac {\sqrt 3} 4×144=36\sqrt 3 \)

接下來將扇形減去正三角形可得弓形面積

\(24\pi－36\sqrt 3 \)

而六弧花的外圍是由12個弓形組成，故先求白色部份面積為

\(12×(24\pi－36\sqrt3)=288\pi－432\sqrt3 \)

最後著色面積為圓面積減去白色面積

\( 144\pi－(288\pi－432\sqrt3)=432\sqrt3－144\pi \) (平方公分)

---

題目提供：陳南羽